GAMES101笔记05-Geometry
Environment Map
Spherical Map
也就是球面映射,把环境光记录在球面上,并且可以将其展开
展开后我们也能发现问题,上下两端的物体会被扭曲,看过时间地图我们就知道,墨卡托投影会将靠两极缩小,靠赤道放大,也就形成了所谓扭曲。
Cube Map
为了解决球面映射的这种扭曲的问题,引入立方体来进行环境光照的纹理映射。从球心到球面的投影向外。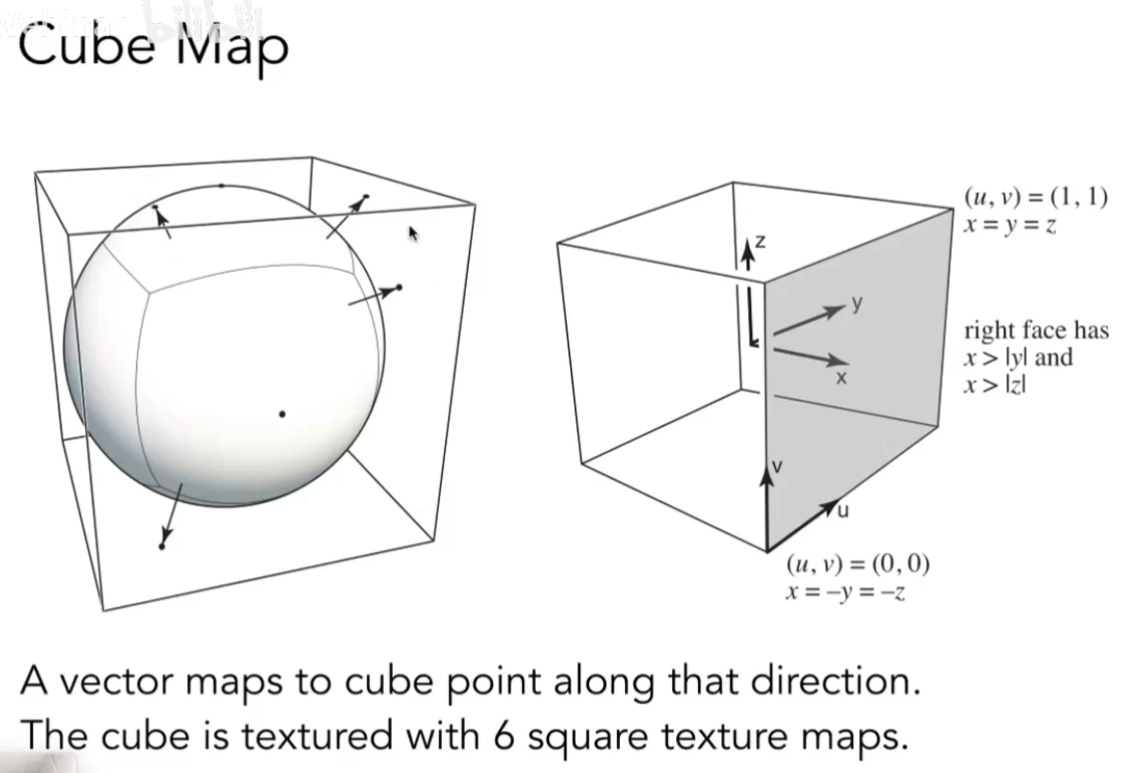
Bump & Displacement Mapping
Bump / Normal Mapping
凹凸贴图,也叫法线贴图。其作用主要为:将每个像素的法线都做一个扰动,高度相对变化,但是不增加三角形面数和改变几何信息。
计算法线贴图(二维)

p点原本的法线是朝上,即n(p) = (0, 1)- 蓝色曲线为使用法线贴图之后的效果
- 通过 $dp = c [h(p + 1) - h(p)]$ 计算出两点的高度差
dp。其中c为定义凹凸贴图影响的程度的常数,h为某点对应高度 - 因此切线就可以表示为
(1, dp) - 切线与法线为垂直关系,所以表示为
n(p) = (-dp, 1)
PS:如何保证法线是 n(p) = (0, 1) ,只需在 TBN 坐标系和世界坐标系之间变换即可
计算法线贴图(三维)
在三维中,有 u ,v 两个方向的变化:
- n(p) = (0, 0, 1)
- $\tfrac{dp}{du} = c_1[h(u + 1) - h(u)]$
- $\tfrac{dp}{dv} = c_2[h(v + 1) - h(v)]$
- n = (-dp / du, -dp / dv, 1).normalized()
Displacement Mapping
即位移贴图,其和凹凸贴图最大的不同在于:它是真的改变了顶点的高度来呈现出凹凸的感觉,但是注意其要求三角形顶点之间的间隔要比纹理定义的频率要高
过程纹理
- 定义空间中任意点的颜色
- 噪声+映射
环境光遮蔽贴图
- 计算好的环境光遮蔽贴图
- 把着色好的结果乘以计算好了的环境光遮蔽纹理
- 说明纹理不止可以储存颜色,还可以储存各种信息
几何的表示
隐式 Implicit
告诉点满足一些特定关系,比如单位球体:$x^2+y^2+z^2=1$。满足一定的关系,并不给出实际的点。通常表示为:$f(x, y, z) = 0$,只要满足这个关系,就代表点在这个表面上面。
- 优点:可以很容易判断某个点在几何体内部,外部或者是其上面
- 缺点:难以通过函数判断几何体的真实形状
显式 Explicit
通过参数映射表示的几何体( uv 坐标转换为 xyz 坐标),例如:
只需将一个一个 u, v 对应过去,即可得到几何形体的形状。
- 优点:容易判断出几何体的真实形状
- 缺点:难以表示出某个点是否在几何体上

几何的隐式表示方法
公式法
可以看出遇到复杂图形时会非常的不直观
CSG(Constructive Solid Geometry)
即构造立体几何法,通过基本几何的集合运算(交并补)来定义新的几何物体
距离函数
距离函数指空间中任意一个点,到想要表述的这个几何形体上面的任意一个点之间的最小距离。可以为正也可以为负的。
例如在下图中,对于上面这种线性融合,我们最终得到的是左边三分之一黑的,中间三分之一灰的,右边三分之一白的。我们想得到的是左边是黑的,右边是白的,它并不能表述出这种运动信息。
下面表示距离函数的图中,可以看到边界处为0。得到了前两张 SDF 图,现在将其混合一下,可以看到正负会被抵消,最终我们得到的边界正好在这张图的中间位置。
距离函数可以通过水平集(Level Set)得到边界,在不同的位置取相同的值,类似于等高线。
分型
递归方法处理自相似,在渲染时会引起强烈的走样
几何的显式表示方法
点云 Point Cloud
- 不考虑物体是一个表面,而是其表面上的一堆点
- 所以就可以表示为一个
x, y, z的列表 - 每个点包含了坐标、颜色等一系列信息
- 应用:激光扫描
多边形网格 Polygon Mesh
- 保存顶点和多边形(通常拆成三角形和四边形)信息
- 图形学中的应用最广泛
如何存储多边形信息
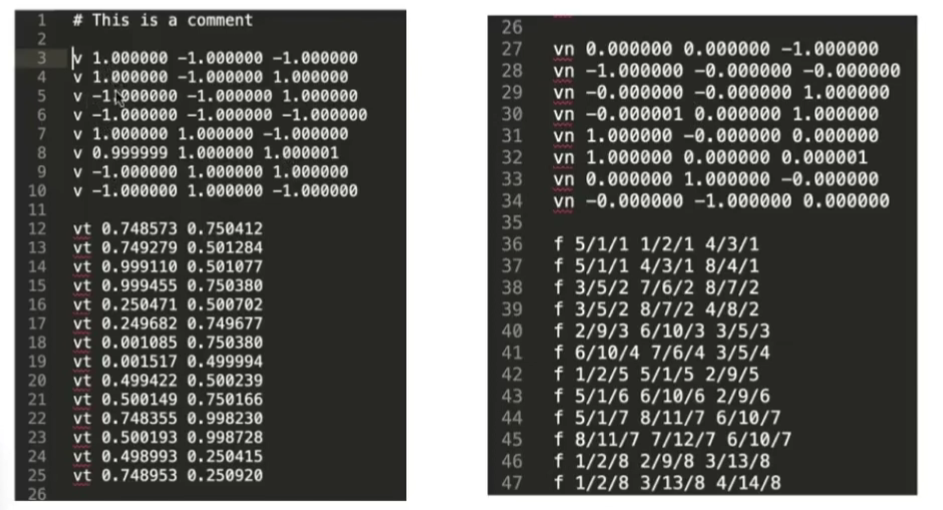
使用 .obj 格式文件,将空间中的一堆顶点,法线,纹理坐标分开表示,然后再一块将其组合起来
如下图所示,定义了一个立方体,有八个顶点 v (x, y, z),六个面的法线 vn (图中有数据冗余),多个纹理坐标 vt ,再使用 f(v/vn/vt) 表示其三个点的关系,如何组成一个三角形
曲线 Curves
贝塞尔曲线 Bézier curve
只要求一定要经过起止点,起止点之间的若干个控制点用于控制曲线弯曲的方向,最终形成一条经过起止点的光滑曲线被成为贝塞尔曲线。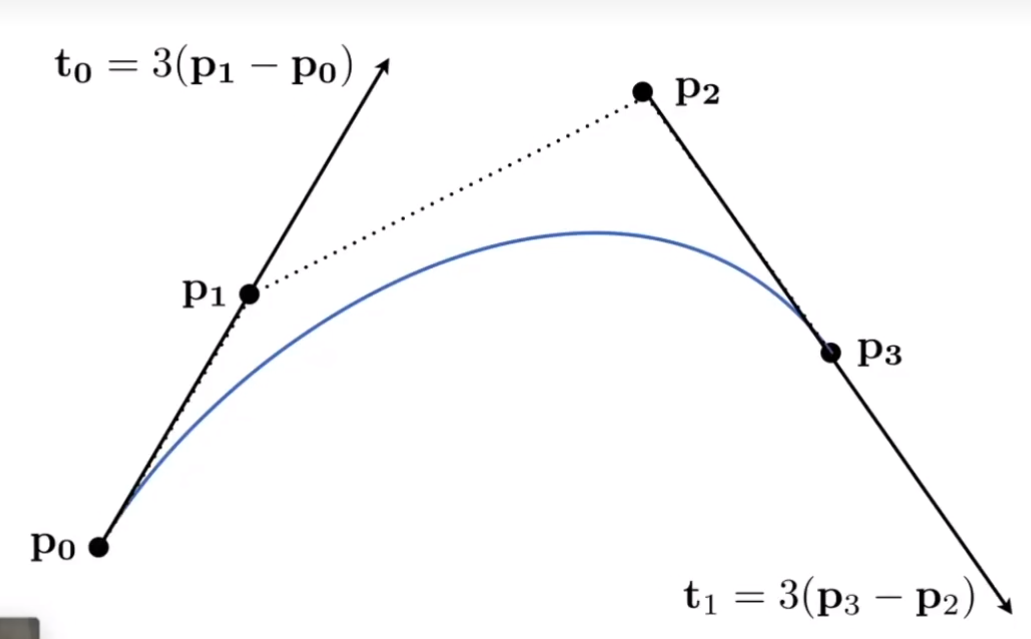
德卡斯特里奥算法 de Casteljau Algorithm
通过德卡斯特里奥算法法来绘制贝塞尔曲线:
- 引入参数
t范围 0 - 1 - 取 $b_0$ 到 $b_1$ ,$b_1$ 到 $b_2$ 上
t位置的点 $b_0^1$ ,$b_1^1$ - 将 $b_0^1$ 和 $b_1^1$ 连接
- 取 $b_0^1$ 和 $b_1^1$ 上
t位置的点 $b_0^2$ - 将
t从 0 到 1 所有的 $b_0^2$ 遍历一份相连即可得到贝塞尔曲线 - 若有
n个控制点则将上面步骤进行递归操作直到找到最终位移 $b_0^n$

总结可得公式:(给出 n + 1 个控制点,分别是从 0 到 n )
其中伯恩斯坦多项式:
贝塞尔曲线的一些性质(n 个控制点的情况):
- $b(0) = b0$ ; $b(1) = b{n - 1}$
- $b^{‘}(0) = 3(b1 - b_0)$ ; $b^{‘}(1) = 3(b{n - 1} - b_{n - 2})$
- 对顶点进行仿射变换,再使用这些控制点得到的贝塞尔曲线和进行仿射变换前是完全相同的,所以如果想对贝塞尔曲线做仿射变换,直接对控制点进行仿射变换之后重新画一条即可
- 对于投影变换则没有类似的性质
- 画出来的贝塞尔曲线一定在控制点形成的凸包之内
凸包
能够包围一系列给定的几何形体的最小的凸多边形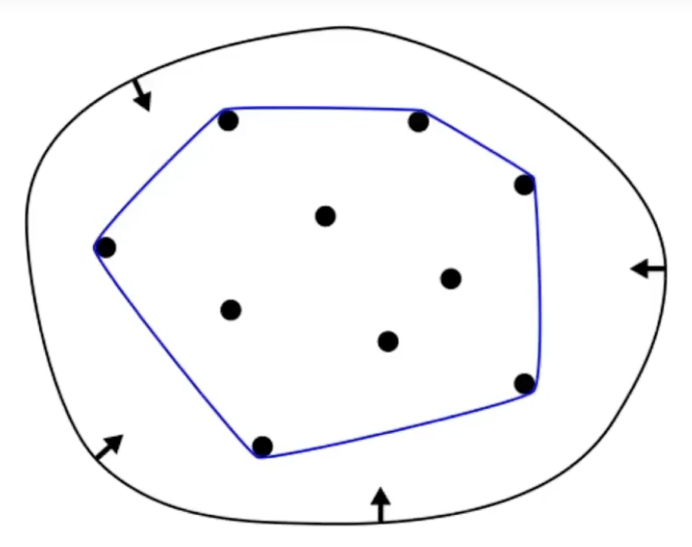
若贝塞尔曲线为一条直线,那么凸包也是一条直线
逐段贝塞尔曲线 Piecewise Bézier Curve
将贝塞尔曲线一段一段来考虑,当控制点太多的时候会影响控制点的效果
使用每四个控制点定义一个贝塞尔曲线,再将其连接起来
如果想使得不同段的贝塞尔曲线平滑过渡,将其相邻的控制点共线即可
C0连续:$a_n = b_0$ 即两曲线收尾连接即可C1连续:$an = b_0 = \tfrac{1}{2} (a{n - 1} + b_{1})$ ,即一阶导数连续C2连续:二阶导数连续
曲面
贝塞尔曲面 Bézier Surface
在两个方向上,分别应用贝塞尔曲线,使用 u, v 替换之前贝塞尔曲线的 t
网格操作 Mesh
分类
- 网格细分
Mesh subdivision:使得网格的面数更多;Loop细分;Catmull-Clark细分 - 网格简化
Mesh simplification:使网格的面数更少;边坍缩;通过“二次误差度量”得到坍缩后最优的点 - 网格正规化
Mesh regularization:让网格中的三角形趋近于正三角形

Loop 细分
分出更多的三角形并使这些三角形的位置发生一点变化
- 将每个三角形分成四个三角形
- 对于不同的权重改变点的位置(新的顶点和老的顶点使用不同的规则)
PS:只能对完全为三角形的几何体进行细分
对于新的顶点
- $V^{‘}$ 为新的顶点变换后的位置
- $A$ , $B$ 为两个面被共享边的的老顶点
- $C$ , $D$ 为非共享边的两个顶点
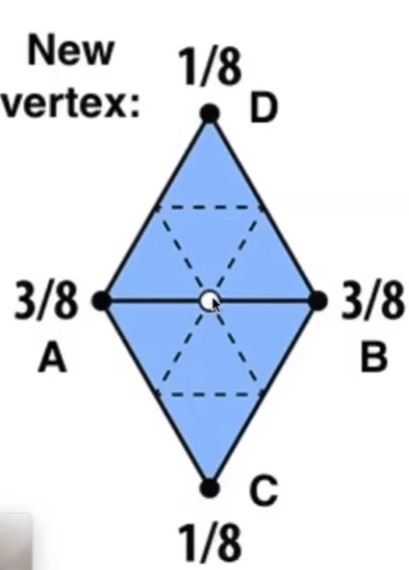
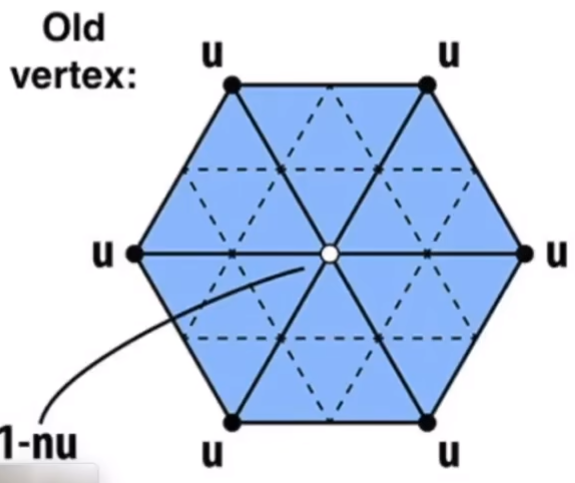
对于老的顶点
其中:
n:顶点的度u:3/16 if n = 3, 3/(8n) otherwiseV'为旧的顶点变换后的位置neighbor_position_sum为邻居点的平均位置original_position为旧顶点原本的位置
Catmull-Clark 细分
可以应用于任意不同的面的细分
奇异点:度不为 4 的点
将面的中点和面的边的中点连起来,在第一次细分之后,非四边形面数量会加到原本奇异点的数量上,之后奇异点不可能再增加了,因为所有的非四边形已经被消除了
点位置更新规则
分为面上的中点(f)、边上的中点(e)、老的顶点(v)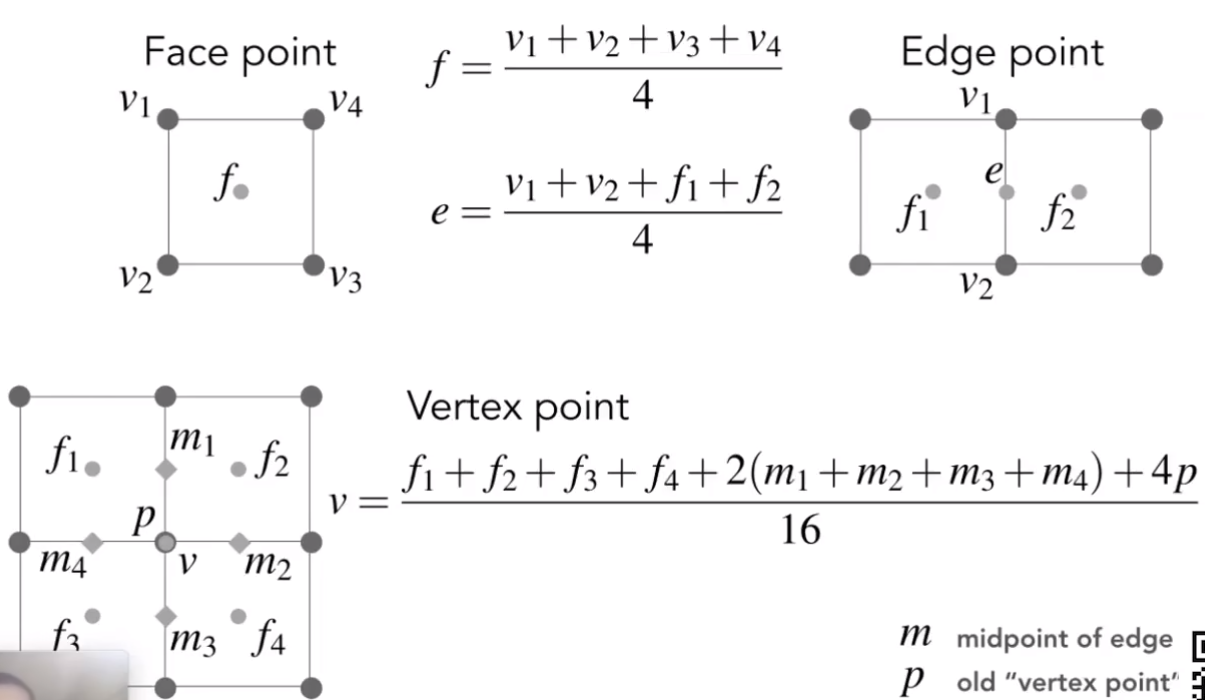
边坍缩算法 edge collapsing
一条边连着两个顶点,把这两个顶点往中间一捏捏成一个顶点,这条边就不再存在了。
面临问题:
- 应该坍缩哪些面,如何界定面的优先级,即哪些不重要哪些重要
- 坍缩之后的订单如何描述
二次误差度量 Quadric Error Metrics

坍缩以后这一个新的顶点和原本几个面都有关系,那么就要求这个点到原本的这几个面的距离的平方和最小
边坍缩算法的步骤
- 对每条边打一个分数,分数就是其坍缩后的二次度量误差
- 对分数最小(误差最小)的边做坍缩,考虑到坍缩后会影响其相邻的边,因此可以使用堆数据结构来维护分数最小的边
Shadow
Shadow Mapping
Key idea: 如果一个点不在阴影里,说明摄像头能看到这个点,并且光源也能看到这个点









