GAMES101笔记 03-反走样和深度缓冲
1 反走样(Antialiasing)
1.1 走样
走样,即锯齿,是因为信号时间变化太快以至于采样跟不上变化的速度,出现了频谱混叠
1.2 时域和频域
时域是描述数学函数或物理信号对时间的关系的一种坐标系。
频域是描述信号在频率方面特性时用到的一种坐标系
1.3 傅里叶级数展开
傅里叶变换可以将时域转换为频域,并且时域和频域也可以使用傅里叶变换和其逆变换相互转换
可以将周期函数表示为正余弦的加权和,也就是傅里叶级数展开,随着展开式越多,越来越接近我们想要表达的函数 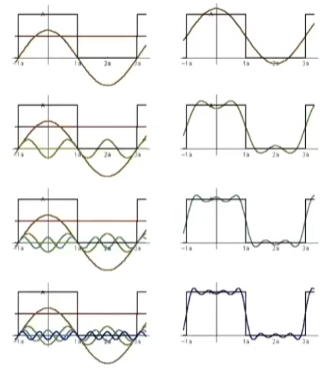
如果采样的频率不够,还原出来的结果就很不精准,无法还原到原函数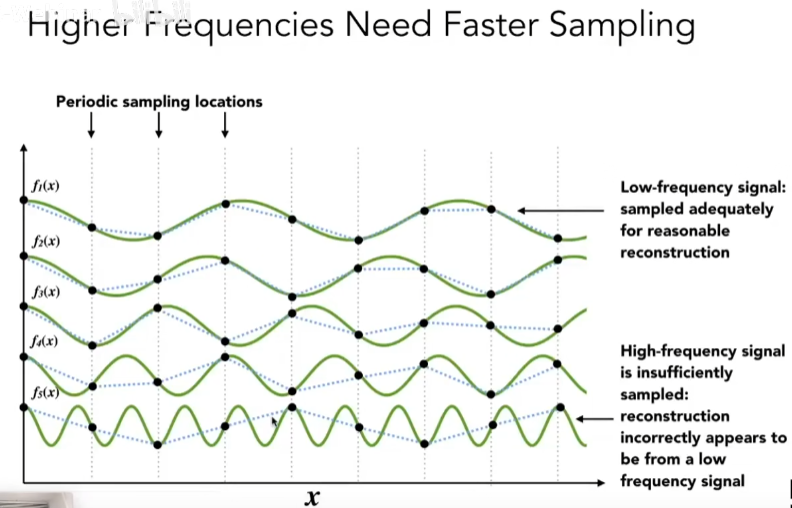
1.4 傅里叶频域图

右图则为左图的傅里叶频域图:
- 中心为低频区,频率由中间向周围放射性状增大,因此外围就为高频区
- 白色代表信息的多少,什么频率的信息越多,那个频率区域白色就会越多
- 为什么会有竖直和水平和两条线:我们在分析一个信号的时候,会认为它是一个周期性的信号,我们认为这张图到了右边界之后又重复左边界的信息,在这个边界变换时,就会发生剧烈的信号变换,就会产生一个极其高的高频
1.5 滤波(Filtering)
滤波,即去掉一些频率的内容,我们还是对上面那两张图做高通和低通滤波
高通滤波
此时只剩下了高频的信息,我们可以看到高频信息其实表示的就是图像的边界
PS:边界就是图形中某个地方,它的上边和下边或者左边和右边发生了一个突变,这个时候就认为这里是边界
低通滤波
也就是模糊了边界(去除了高频信号)
1.6 卷积
滤波=卷积(=平均)
简化一下定义:卷积的结果就是相邻数取平均值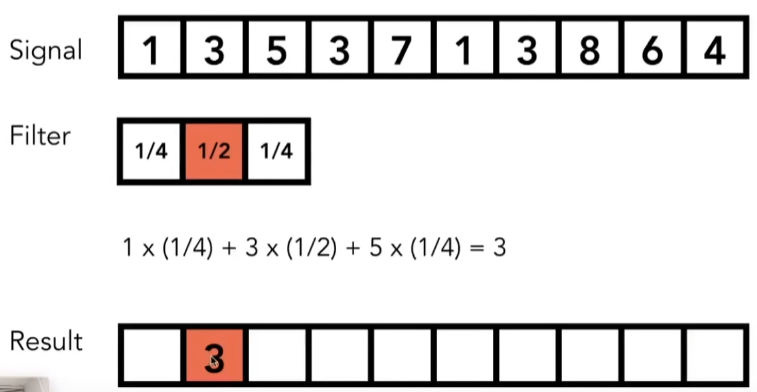
定理:时域的卷积等于频域的乘积
1.7 频谱混叠

首先看一下这张图,这就是为什么会走样,由于采样的频率不够(稀疏采样),出现了频谱混叠,而我们使用密集采样时,就不容易出现走样。
再来看下这张图,我们使用低频滤波去掉了一部分的高频信号,可以看到时域图上被剪切的部分就是高频信号。去掉之后,这个频谱在对应位置就不再发生混叠了,减少了走样,我们以失去一部分高频信息(边界)为代价,也就是模糊处理,换来了走样的减少。
PS:同时也能解释为什么要先滤波再采样,如果我们先采样再使用滤波去除每个频谱混叠的区域时,那丢失的信息太多了
1.8 反走样(抗锯齿)
反走样的流程:
- 通过将每个像素进行模糊卷积处理
- 再对每个像素中心进行采样
在光栅化一个三角形时,像素颜色的平均值f(x,y)= 三角形的覆盖像素的面积
1.9 超采样(MSAA)
MSAA: Antialiasing By Supersampling
在游戏中的抗锯齿选项可能也见过这个MSAA,它的原理是:将每个像素划分为更小的几个像素,再进行模糊处理,缺点就是运算量太大了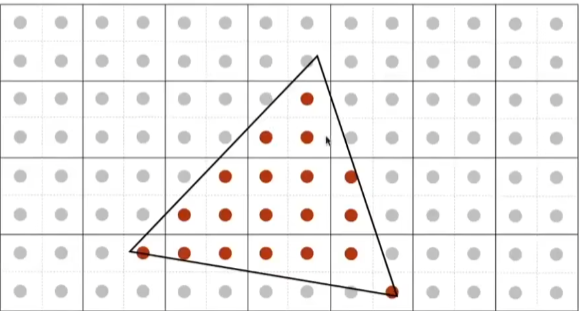
(MSAA X4)
2 深度缓冲(Z-Buffering)
2.1 画家原理
我们试想一下,在将物体光栅化的过程中,肯定有近的物体覆盖住远的物体,那么如何去确定呢?根据画家画画的原理,肯定是先画远处的物体再画近处的物体,这样就能确定有重叠的情况肯定是近的物体确定远的物体
但是如果遇到以下这种情况就无法确定了: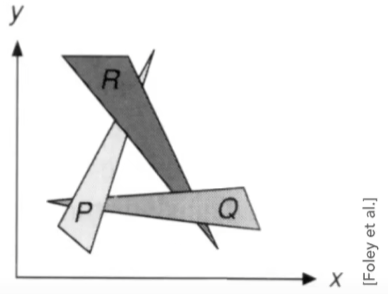
所以就需要深度缓冲
2.2 Z-Buffering
每一帧光栅化渲染时,我们需要同步渲染frame buffer和depth buffer(z-buffer)
- frame buffer:最终的结果
- depth buffer:当前看到的场景任何一个像素对应的深度
PS:单纯对深度来说,假设z值都是正的
2.3 Z-buffer algorithm
时间复杂度 $O(n)$,常数根据三角形内的像素点决定
PS:因为z是浮点数,一般情况下不会出现像素深度相等的情况
initialize depth to $\infin$1
2
3
4
5
6
7for (each triangle T)
for (each sample (x, y, z) in T) // 找到任一三角形覆盖的任一像素
if (z < zbuffer[x, y]) // cloest sample to far
framebuffer[x, y] = rgb; // update color
zbuffer[x, y] = z; // update depth
else
; // do nothing, this sample is occluded









