2D 动画技术

Sprite Animation

把动画每一个动作都记下来，循环播放也就变成了动画。

这种方法可以做到 3D 的效果吗，显然是可以的，请看 DOOM：

DOOM 在各个视角都做了一系列的动作，根据相机的位置，去播放不同的 sprite 动画。来呈现一个 3D 空间中的效果。

这种动画技术在目前的 3D 游戏当中并没有消失，比如粒子系统，有些爆炸以及爆炸带来的烟尘，也是一个个 sprite 序列化组成的。比如《八方旅人》当中也是使用 2D 人物在 3D 场景当中。

Live2D

live2d 会将一个大的整体分为很多小的图源，并且设置每个图源的深度，来描述其遮挡关系。接着会把每一个图片元素，生成一个控制网格，网格上可以随机加入控制点，当对控制点进行操作的时候，图片也就随之去变换。接着 k frame 去变换即可。

3D 动画技术

DOF(Degrees of Freedom)

指一个物体有多少个自由度，可以从多少个维度去变化。在三维空间当中的一个刚体是 6DOF 的：

x, y, z 轴上平移
绕 x, y, z 轴旋转

Rigid Hierarchial Animation

将 mesh 和骨骼绑定，同时骨骼也是一个树状结构的，因此叫 hierarchial，类似于皮影戏，去转动每个骨骼的关节。但是有一个问题：在骨骼动的时候，mesh 之间会相互穿插。

Per-vertex Animation

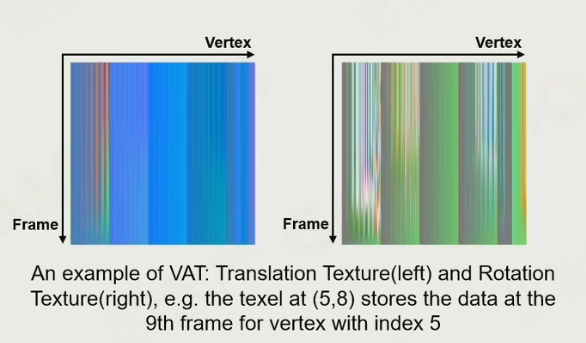
比如要做一个旗帜飘动的动画，如果要绑骨骼，工作量是非常大的。因此直接把每个顶点的位置存下来。此时一般会存两个 texture，texture 的横向轴就代表一个顶点，数轴就是存其每一帧的 offset。但是顶点变了法线也会改变，这时候就需要再存一下法线的 offset。这种 texture 一般是使用物理引擎离线模拟出来的。

3D Skinned Animation

如果有了一个模型网格，如何使其动起来：

制作一个在 bindind pose 下的网格模型
制作骨骼，内嵌在皮肤之下，与网格模型对齐
对其进行蒙皮，也就是对与网格模型的每个顶点，确定其受哪些骨骼的影响且受哪些骨骼的影响更大
制作 animation

Different Spaces

在这里先要提一下三个空间，动画系统当中的所有计算都是在其各自的空间当中：

Model Space：以模型自己为中心的坐标系，比如人面前 2 立方米的空间，其与 World Space 并不是应该简单的平移关系，因为坐标系的朝向也可能发生变化。
Local Space：指的是每一根骨骼（关节点）之间存在平移和旋转，相对于 Model Space 又发生了变化。每个关节点的坐标系都是不同的。比如对于手指尖关节，需要根据根节点坐标系依次传递到手指尖，才能知道其在 World Space 当中的朝向
World Space：世界坐标系

整个动画数据，实际上都是存储在 Local Space 当中的，把 Local Space 从根节点积分（累算）才能得到 Model Space 的数据。接着考虑角色自身的平移，旋转，才能得到其 World Space。这个角色才会被渲染。

在 Humaniod 这种形体建模的时候，一般是会将其起点设置在人的胯部（Pelvis），即脊椎的最后一块骨头上面。

Joint & Bone

此处需要明确一个概念，上面所说的一些骨骼，并不是指真正一条一条的骨骼，而是关节（Joint），两个关节之前定义了骨骼，实际上存储的是关节数据。因为关节连接了一个刚体的骨骼，当关节发生旋转或者平移的时候，骨骼也就随之变化。关节有很多自由度，但是骨骼是没有的，因为骨骼是两个关节联合在一起去定义的。比如：当小臂肌肉扭曲时，可以使用关节进行表达，但是无法使用骨骼去表达。

比如角色手里要拿一把斧头，就可以在其手部添加一个 Weapon Mount Joint 的关节点，所有武器都会被绑定到上面，看起来就像手里拿了武器。

一个模型有位于 Pelvis 的起点，同时也有一个 Root 关节，在 Humaniod 里面，一般是定义在两脚之间的位置。这是因为比如要表达一个角色跳跃的动作，然后离地高度设置为 0.5m，如果使用 Pelvis 来存储的花，其下蹲和跳跃都会改变离地高度，而离地是指角色脚到地面的高度，因此从其 Root 出发。

考虑一个动画绑定的场景，比如人骑在马上，人与马的动画是分开的，靠绑定其点 x, y, z 空间位置以及朝向，来实现两者对其。