立方体的组合

在 Unity基础补全Mesh01——网格的生成当中，我们了解了如何去使用 mesh 生成一个 2D 的网格，接下来我们使用 mesh 来生成一个 3D 结构，比如最常见的立方体，其是由 6 个 2D 平面构成的。

上一篇博客当中网格是位于的 XY 平面，面对的是 -Z 方向，换算到 3D 结构当中，就是立方体的 -Z 面，那要创造其相对的 +Z 面，把 -Z 面绕 Y 轴旋转 180° 即可。

-X 和 +X 面的创建过程类似，只不过是将 -Z 绕 Y 轴旋转 90° 和 270°。其 ySize 应该与 Z 面匹配。

而到了 -Y 和 +Y 的时候，则是绕其 X 轴旋转 270° 和 90°，它们的 xSize 应该与 Z面的 xSize 匹配，它们的 ySize 应该匹配 X面的 xSize。

创建立方体顶点集合

首先，我们提供一个脚本模板，类似于前一章当中的脚本：

使用协程来可视化顶点构建顺序
使用 Gizmos 来绘画顶点所在 Scene 中的位置

[RequireComponent(typeof(MeshFilter), typeof(MeshRenderer))]
public class CubeMesh : MonoBehaviour
{
    public int xSize, ySize, zSize;

    private Mesh _mesh;
    private Vector3[] _vertices;

    private void Awake()
    {
        StartCoroutine(Generate());
    }

    private IEnumerator Generate()
    {
        _mesh = new Mesh();
        GetComponent<MeshFilter>().mesh = _mesh;
        _mesh.name = "Procedural Cube";

        yield return new WaitForSeconds(0.05f);
    }

    private void OnDrawGizmos()
    {
        if (_vertices == null)
        {
            return;
        }

        Gizmos.color = Color.black;
        for (int i = 0; i < _vertices.Length; i++)
        {
            Gizmos.DrawSphere(_vertices[i], 0.1f);
        }
    }
}

接着我们给出一组数据：

xSize = 3
ySize = 2
zSize = 4

注意：此处的 size 指的是网格的数量而非顶点的数量

因为立方体当中，边和点都是 2 个或者 3 个面共用的，那么我们就来分析一下三种不同类型的顶点：

8 个角点，分布在立方体的角上，是由三个面共用的
在每一条边上，除开最边缘的两个角点，中间的 n - 2（n 为当前边上顶点个数）点是由两个面共享的
除开前两种情况，在每一个面的中央，其顶点是由单个面独有的。

其实顶点重复是非常常见的，它会被用来在一个有法线的 Mesh 中创建锋利的边缘。因此，我们确实可以创建完全独立的六个面，只是数据组合在一个数组中而已。但是此处我们并不会创建出重复顶点。

接下来我们就可以得出顶点的数量：

int cornerVertices = 8;
int edgeVertices = (xSize + ySize + zSize - 3) * 4;
int faceVertices = ((xSize - 1) * (ySize - 1) +
                    (xSize - 1) * (zSize - 1) +
                    (ySize - 1) * (zSize - 1)) * 2;
_vertices = new Vector3[cornerVertices + edgeVertices + faceVertices];

定位第一面行的顶点：

int v = 0;
for (int x = 0; x <= xSize; x++)
{
    _vertices[v++] = new Vector3(x, 0, 0);
    yield return new WaitForSeconds(0.05f);
}

依次类推，总共创建出四次循环，创建一个方形的顶点环：

int v = 0;
for (int x = 0; x <= xSize; x++)
{
    _vertices[v++] = new Vector3(x, 0, 0);
    yield return new WaitForSeconds(0.05f);
}

for (int z = 1; z <= zSize; z++)
{
    _vertices[v++] = new Vector3(xSize, 0, z);
    yield return new WaitForSeconds(0.05f);
}

for (int x = xSize - 1; x >= 0; x--)
{
    _vertices[v++] = new Vector3(x, 0, zSize);
    yield return new WaitForSeconds(0.05f);
}

// 注意此处 z 不能等于 0，原点最开始已经有点了
for (int z = zSize - 1; z > 0; z--)
{
    _vertices[v++] = new Vector3(0, 0, z);
    yield return new WaitForSeconds(0.05f);
}

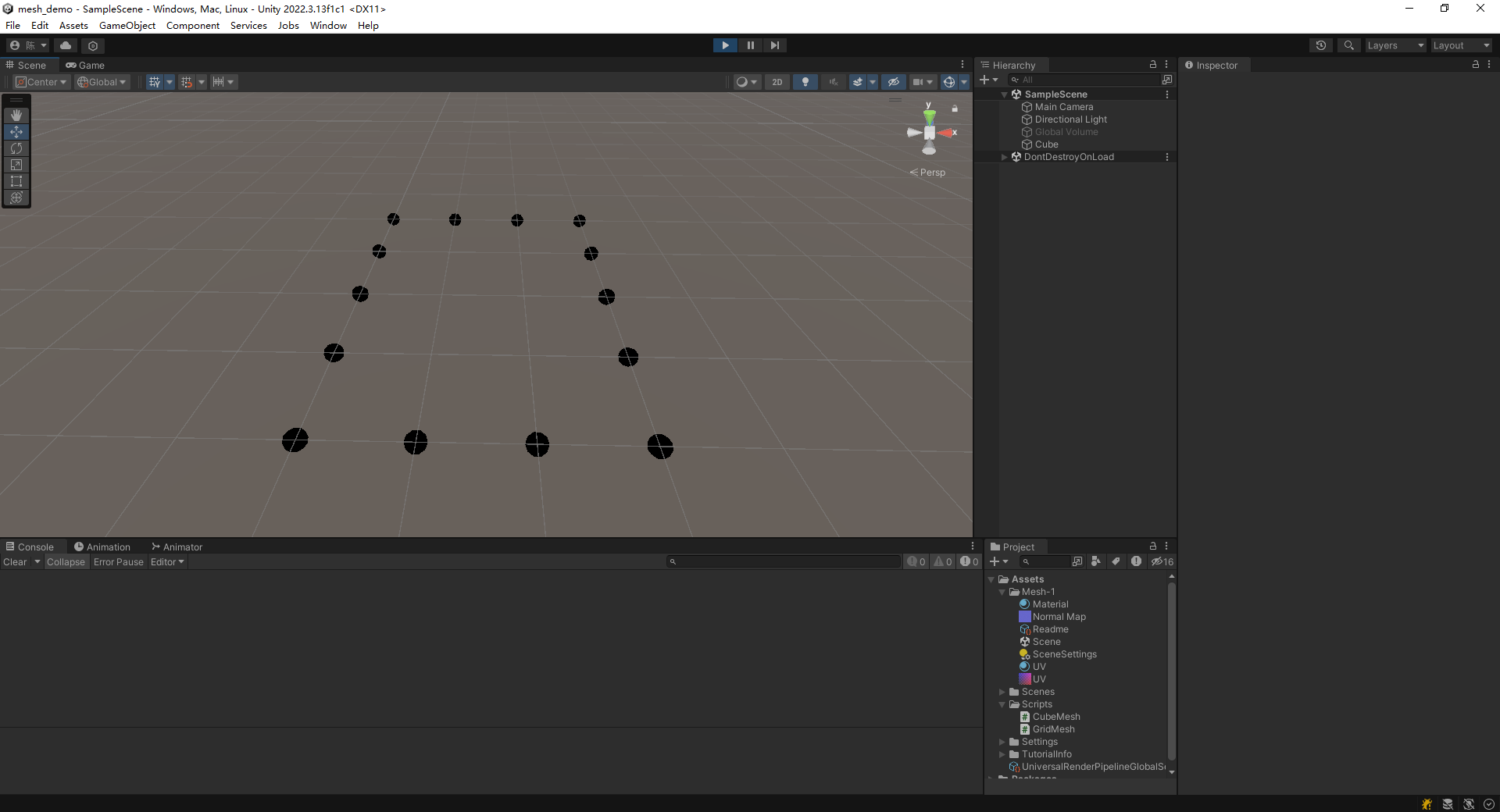
接着在 Y 方向上重复上面四个循环的操作，就能构建琪 3D 结构最外围的一块：

int v = 0;
for (int y = 0; y <= ySize; y++)
{
    for (int x = 0; x <= xSize; x++)
    {
        _vertices[v++] = new Vector3(x, y, 0);
        yield return new WaitForSeconds(0.05f);
    }

    for (int z = 1; z <= zSize; z++)
    {
        _vertices[v++] = new Vector3(xSize, y, z);
        yield return new WaitForSeconds(0.05f);
    }

    for (int x = xSize - 1; x >= 0; x--)
    {
        _vertices[v++] = new Vector3(x, y, zSize);
        yield return new WaitForSeconds(0.05f);
    }

    for (int z = zSize - 1; z > 0; z--)
    {
        _vertices[v++] = new Vector3(0, y, z);
        yield return new WaitForSeconds(0.05f);
    }
}

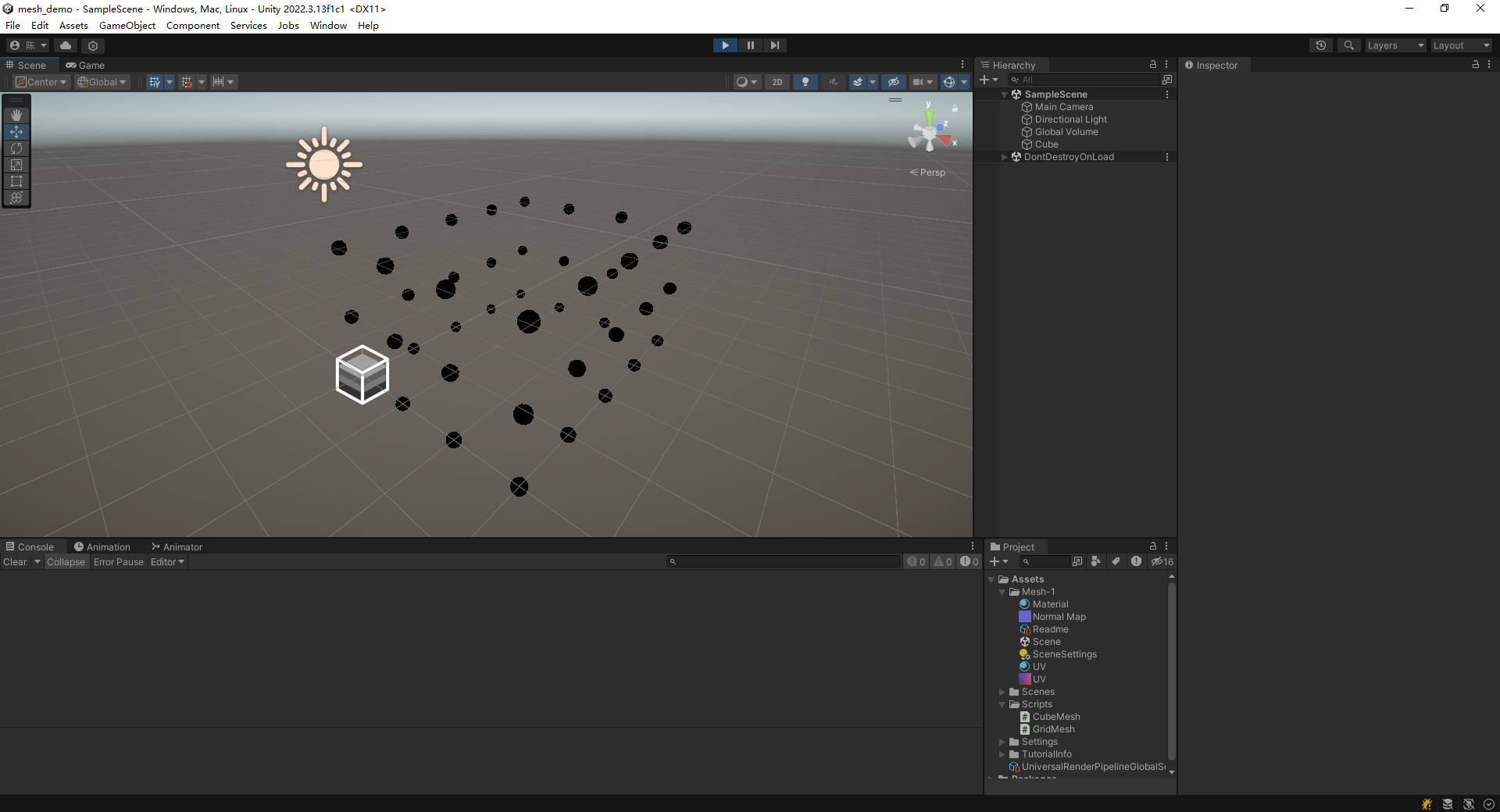
最后在底部和顶部盖上盖子：

int v = 0;
for (int y = 0; y <= ySize; y++)
{
    for (int x = 0; x <= xSize; x++)
    {
        _vertices[v++] = new Vector3(x, y, 0);
        yield return new WaitForSeconds(0.05f);
    }

    for (int z = 1; z <= zSize; z++)
    {
        _vertices[v++] = new Vector3(xSize, y, z);
        yield return new WaitForSeconds(0.05f);
    }

    for (int x = xSize - 1; x >= 0; x--)
    {
        _vertices[v++] = new Vector3(x, y, zSize);
        yield return new WaitForSeconds(0.05f);
    }

    for (int z = zSize - 1; z > 0; z--)
    {
        _vertices[v++] = new Vector3(0, y, z);
        yield return new WaitForSeconds(0.05f);
    }
}

for (int z = 1; z < zSize; z++)
{
    for (int x = 1; x < xSize; x++)
    {
        _vertices[v++] = new Vector3(x, ySize, z);
        yield return new WaitForSeconds(0.05f);
    }
}

for (int z = 1; z < zSize; z++)
{
    for (int x = 1; x < xSize; x++)
    {
        _vertices[v++] = new Vector3(x, 0, z);
        yield return new WaitForSeconds(0.05f);
    }
}

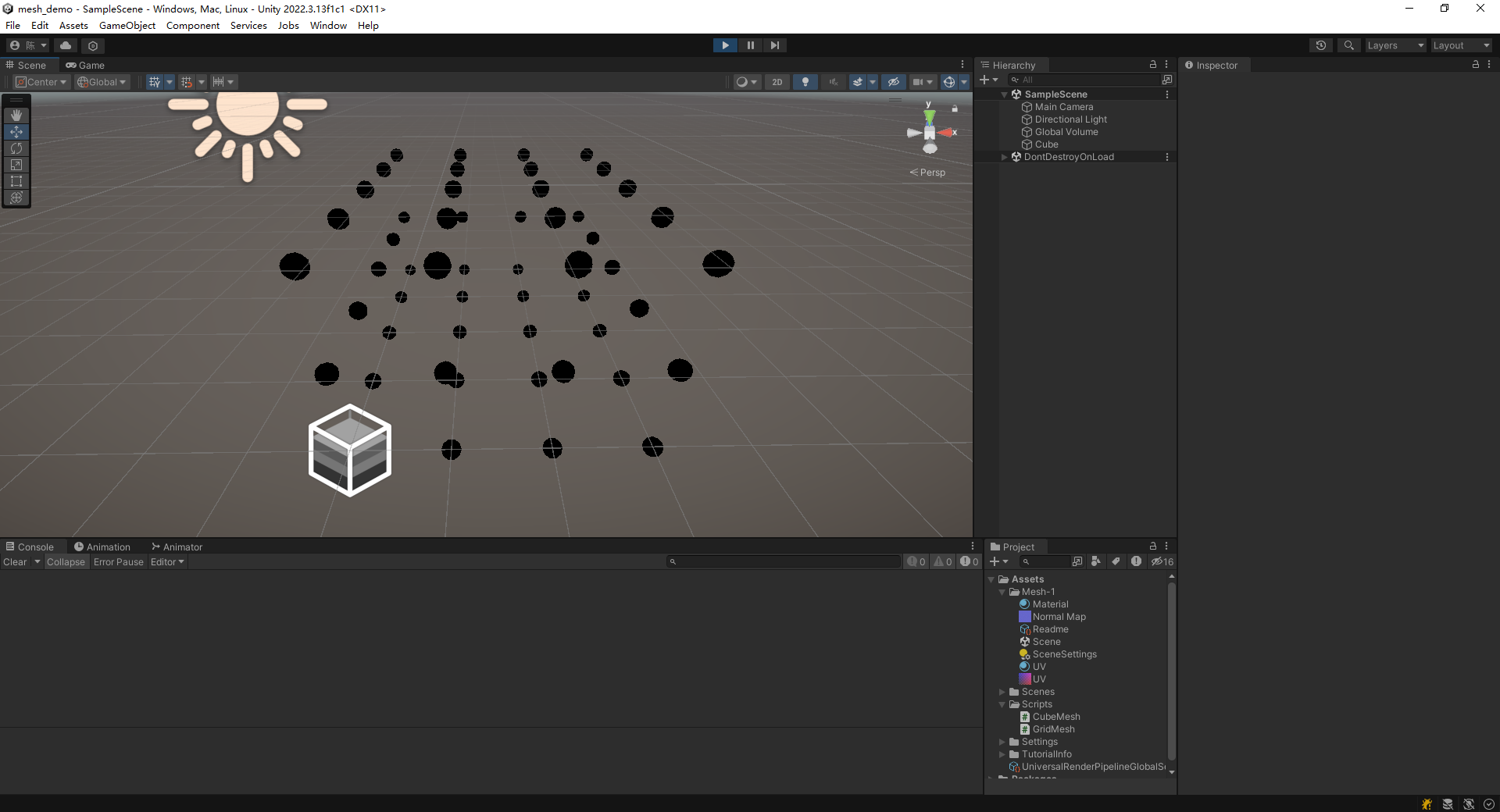
这样就构建起了所有顶点了。

添加三角形

此处我们先抛弃协程，封装一些单独方法：

private void Awake()
{
    Generate();
}
private void Generate()
{
    _mesh = new Mesh();
    GetComponent<MeshFilter>().mesh = _mesh;
    _mesh.name = "Procedural Cube";
    CreateVertices();
    CreateTriangles();
}
private void CreateVertices()
{
    // ...
    _mesh.vertices = _vertices;
}
private void CreateTriangles() {}

接着提取出一个创建正方形的通用方法：

private static int SetQuad(int[] triangles, int i, int v00, int v10, int v01, int v11)
{
    triangles[i] = v00;
    triangles[i + 4] = triangles[i + 1] = v01;
    triangles[i + 3] = triangles[i + 2] = v10;
    triangles[i + 5] = v11;

    return i + 6;
}

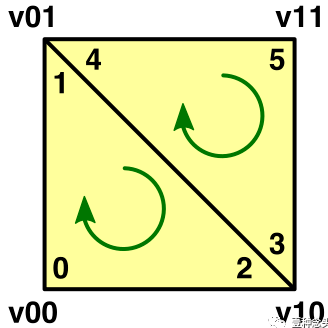
（四边形的顺时针顺序）

此处使用三角形顶点索引数组传参
此处返回三角形顶点索引数组的 index，这样每次设置四边形时，只要将结果分配给索引就可以了。

首先尝试一下创建出正对面第一排正方形，和上一章唯一的区别在于：下一行中顶点的偏移量等于一个完整的顶点环（即 (xSize + zSize) * 2）。

private void CreateTriangles()
{
    // 正方体的总个数
    int quads = (xSize * ySize + xSize * zSize + ySize * zSize) * 2;
    // 三角形顶点的数量，一个正方形有两个三角形所以是 六个 顶点索引
    int[] triangles = new int[quads * 6];
    // 因为上面的顶点是一层一层网格环状生成的，因此此处是 x，z 轴个数加起来乘 2
    int ring = (xSize + zSize) * 2;
    int t = 0, v = 0;
    for (int q = 0; q < xSize; q++, v++)
    {
        t = SetQuad(triangles, t, v, v + 1, v + ring, v + ring + 1);
    }

    _mesh.triangles = triangles;
}

如果要将最下面一层使用正方形包围起来的话，首先可能想到的是，将 q 的遍历范围改为 (0, ring)：

for (int q = 0; q < ring; q++, v++)
{
    t = SetQuad(triangles, t, v, v + 1, v + ring, v + ring + 1);
}

结果就是，除了最后一个正方形其他看起来都是正确的。这是因为，最后一个正方形，其第二和第四个点，应该是要回到环开始的地方。

for (int q = 0; q < ring - 1; q++, v++)
{
    t = SetQuad(triangles, t, v, v + 1, v + ring, v + ring + 1);
}
t = SetQuad(triangles, t, v, v + 1 - ring, v + ring, v + 1);

到此为止，环看起来就很正常了。同样类似于上面创建顶点的办法，要使得侧面都被正方形包围我们只需要在 Y 方向上重复这个操作即可。

for (int y = 0; y < ySize; y++, v++)
{
    for (int q = 0; q < ring - 1; q++, v++)
    {
        t = SetQuad(triangles, t, v, v + 1, v + ring, v + ring + 1);
    }
    t = SetQuad(triangles, t, v, v + 1 - ring, v + ring, v + 1);
}

接着是顶部面的创建，首先我们来通过一张图清晰了解一下顶部的顶点结构（这张图对理解代码很重要）：

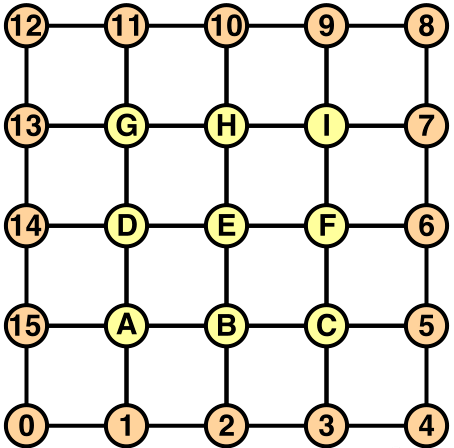
接着我们首先来完成顶层第一排的创建工作（此处也是提取出了一个独立的方法）：

private int CreateTopFace(int[] triangles, int t, int ring)
{
    // 找到最顶层的第一个顶点，也就是从上往下看左下角
    int v = ring * ySize;
    for (int x = 0; x < xSize - 1; x++, v++)
    {
        t = SetQuad(triangles, t, v, v + 1, v + ring - 1, v + ring);
    }
    t = SetQuad(triangles, t, v, v + 1, v + ring - 1, v + 2);

    return t;
}

接着是第二行：

int vMin = ring * (ySize + 1) - 1; // 对应图中的 15
int vMid = vMin + 1;               // 对应图中的 A
int vMax = v + 2;                  // 对应图中的 5
t = SetQuad(triangles, t, vMin, vMid, vMin - 1, vMid + xSize - 1);

for (int x = 1; x < xSize - 1; x++, vMid++)
{
    t = SetQuad(triangles, t, vMid, vMid + 1, vMid + xSize - 1, vMid + xSize);
}
t = SetQuad(triangles, t, vMid, vMax, vMid + xSize - 1, vMax + 1);

此处我们可以使用一个循环来处理除最后一行以外的所有行（因为此处环的走向，vMid 和 vMax 都会增大，而 vMin 反而会减小）：

int vMin = ring * (ySize + 1) - 1; // 对应图中的 15
int vMid = vMin + 1;               // 对应图中的 A
int vMax = v + 2;                  // 对应图中的 5

for (int z = 1; z < zSize - 1; z++, vMin--, vMid++, vMax++)
{
    t = SetQuad(triangles, t, vMin, vMid, vMin - 1, vMid + xSize - 1);
    for (int x = 1; x < xSize - 1; x++, vMid++)
    {
        t = SetQuad(triangles, t, vMid, vMid + 1, vMid + xSize - 1, vMid + xSize);
    }
    t = SetQuad(triangles, t, vMid, vMax, vMid + xSize - 1, vMax + 1);
}

到了最后一行，此处也是分成第一个，中间，最后一个三部分去处理正方形的构成，首先是第一个正方形：

1
2
3

// 最后一行（注意此时 vMin 为图中 13）
int vTop = vMin - 2;
t = SetQuad(triangles, t, vMin, vMid, vTop + 1, vTop);

接着是中间的正方形：

for (int x = 1; x < xSize - 1; x++, vTop--, vMid++)
{
    t = SetQuad(triangles, t, vMid, vMid + 1, vTop, vTop - 1);
}

最后是最后一个正方形：

1	t = SetQuad(triangles, t, vMid, vTop - 2, vTop, vTop - 1);

最终，我们就完成了立方体顶面的创建：

其实此处有那个排布图就还是比较好理解，重点就在于找到最开始的基准点和循环更新以后基准点的位置变化。

接下来是底面正方形第一排，我们使用一张图就能很清晰看懂逻辑了，大体和顶面一样，不同的是三角形面朝向要向下，改变其时钟方向，此处来一张图更好理解：

private int CreateBottomFace(int[] triangles, int t, int ring)
{
    // 此时 ring 为第二层外围第一个元素
    int v = 1; // 对应图中的 1
    int vMid = _vertices.Length - (xSize - 1) * (zSize - 1); // 对应底面内层第一个顶点
    t = SetQuad(triangles, t, ring - 1, vMid, v - 1, v);
    for (int x = 1; x < xSize - 1; x++, v++, vMid++)
    {
        t = SetQuad(triangles, t, vMid, vMid + 1, v, v + 1);
    }
    t = SetQuad(triangles, t, vMid, v + 2, v, v + 1);
    
    // ...
}

接下来是中间部分，同样此处给出基准点开始位置的可视化图片：

int vMin = ring - 2;
vMid -= xSize - 2;   // 将 vMid 从内层第一排末尾搬到内层第一排开始的地方
int vMax = v + 2;

for (int z = 1; z < zSize - 1; z++, vMin--, vMid++, vMax++)
{
    t = SetQuad(triangles, t, vMin, vMid + xSize - 1, vMin + 1, vMid);
    for (int x = 1; x < xSize - 1; x++, vMid++)
    {
        t = SetQuad(triangles, t, vMid + xSize - 1, vMid + xSize, vMid, vMid + 1);
    }
    t = SetQuad(triangles, t, vMid + xSize - 1, vMax + 1, vMid, vMax);
}

最后是最后一行的部分，所以创建表面的工作就到此结束了：

int vTop = vMin - 1;
t = SetQuad(triangles, t, vTop + 1, vTop, vTop + 2, vMid);
for (int x = 1; x < xSize - 1; x++, vTop--, vMid++)
{
    t = SetQuad(triangles, t, vTop, vTop - 1, vMid, vMid + 1);
}
t = SetQuad(triangles, t, vTop, vTop - 1, vMid, vTop - 2);