Unity基础补全Mesh01——网格的生成
概念
为什么需要 mesh?在 unity 当中,是基于 mesh 去渲染的。mesh 是指模型的网格,主要属性会包括:
- 顶点坐标集合
- 连接这些点的三角形(三角形绘制序列)
- 法线
- 纹理坐标
- …
而在 unity 当中如果要渲染一个 3D 物体的话,就需要两个 component:
Mesh Filter:包含一个Mesh组件,可以获取也可以取出。Mesh Render:渲染网格的组件,其作用就是将Mesh Filter指定的网格渲染出来,还有指定使用什么材质球之类的设置。
生成网格
创建顶点网格
直接创建一个 Vector3[] 对象来存储我们所以的顶点信息。1
2
3
4
5
6
7
8_vertices = new Vector3[(xSize + 1) * (ySize + 1)];
for (int i = 0, y = 0; y <= ySize; y++)
{
for (int x = 0; x <= xSize; x++, i++)
{
_vertices[i] = new Vector3(x, y);
}
}
此处的 xSize,ySize 分别代表其顶点在 x 轴方向和 y 轴方向的数量,因此 $3X5$ 的顶点数量表示的就是 $2X4$ 数量的方格。
关于验证顶点生成的正确性(数量,顺序):可以直接使用 Gizmos 加协程画出来即可
创建 mesh 以及定义三角形
在前面提到了我们渲染指定的网格是由 Mesh Filter 指定的,而重点也就是其中的 Mesh 组件,此处我们只需设置即可。1
2Mesh mesh = new Mesh();
GetComponent<MeshFilter>().mesh = mesh;
这样在运行时就能在挂载的 GameObject 上面看到我们运行时生成的 mesh 了。但是发现并不能看到它,因为我们还没有定义网格的三角形,
三角形是由一系列顶点索引来定义的,通俗来说也就是我们 Mesh.vertices 的 index 来索引的。三个连续的索引点就描述了一个三角形。例如:1
2
3
4
5int[] triangles = {
0,
1,
2,
};
接着设置好 mesh 的 triangles。进入发现并没有被渲染出来,因为三个点都是在一条直线上面,三角形退化成了直线。
接着我们又改动代码为:1
2
3
4
5int[] triangles = {
0,
1,
xSize + 1,
}
很出人意料的是,三角形仍然没有被渲染出来,这就是此处的重点了。
三角形的哪一边可见是由它的顶点顺序的时钟方向决定的。默认情况下,顺时针排布的三角形是被认为是前向的,可见的,而逆时针排布的三角形则被丢弃,因为并不会花时间去渲染模型内部的三角形面,因为通常都是不可见的。(也就是说,上面这个三角形排布,我们只能从 z 轴负方向才能观测到)。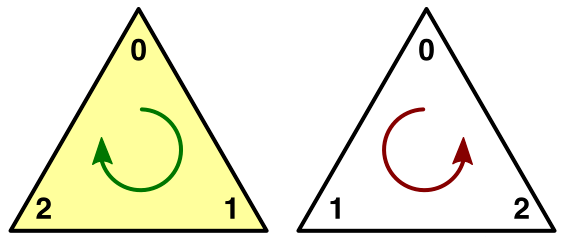
将代码改为:1
2
3
4
5int[] triangles = {
0,
xSize + 1,
1
};
就能正常被渲染出来了。
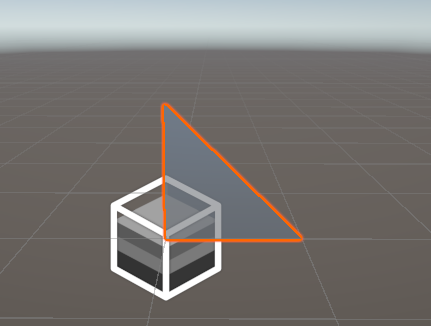
为了能铺满这一块网格,我们再添加一组三角形的索引,此处两个三角形共用中间的一条边,因此我们此处右上的三角形有两个点是可以和左下的共用的,也就是 index 之间的对应关系:
1对应42对应3
1 | int[] triangles = { |
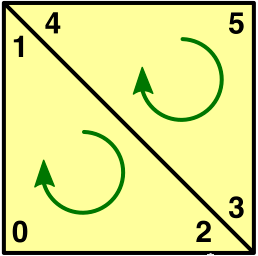
接下来填充所有的网格:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18int[] triangles = new int[xSize * ySize * 6];
// ti 代表三角形下标索引,一次性更新 6 个
// vi 代表当前正方形左下角的顶点索引
for (int ti = 0, vi = 0, y = 0; y < ySize; y++, vi++)
{
for (int x = 0; x < xSize; x++, ti += 6, vi++)
{
triangles[ti] = vi;
triangles[ti + 4] = triangles[ti + 1] = vi + xSize + 1;
triangles[ti + 3] = triangles[ti + 2] = vi + 1;
triangles[ti + 5] = vi + xSize + 2;
}
}
// 最后来设置一下 mesh
_mesh.vertices = _vertices;
_mesh.triangles = triangles;
GetComponent<MeshFilter>().mesh = _mesh;
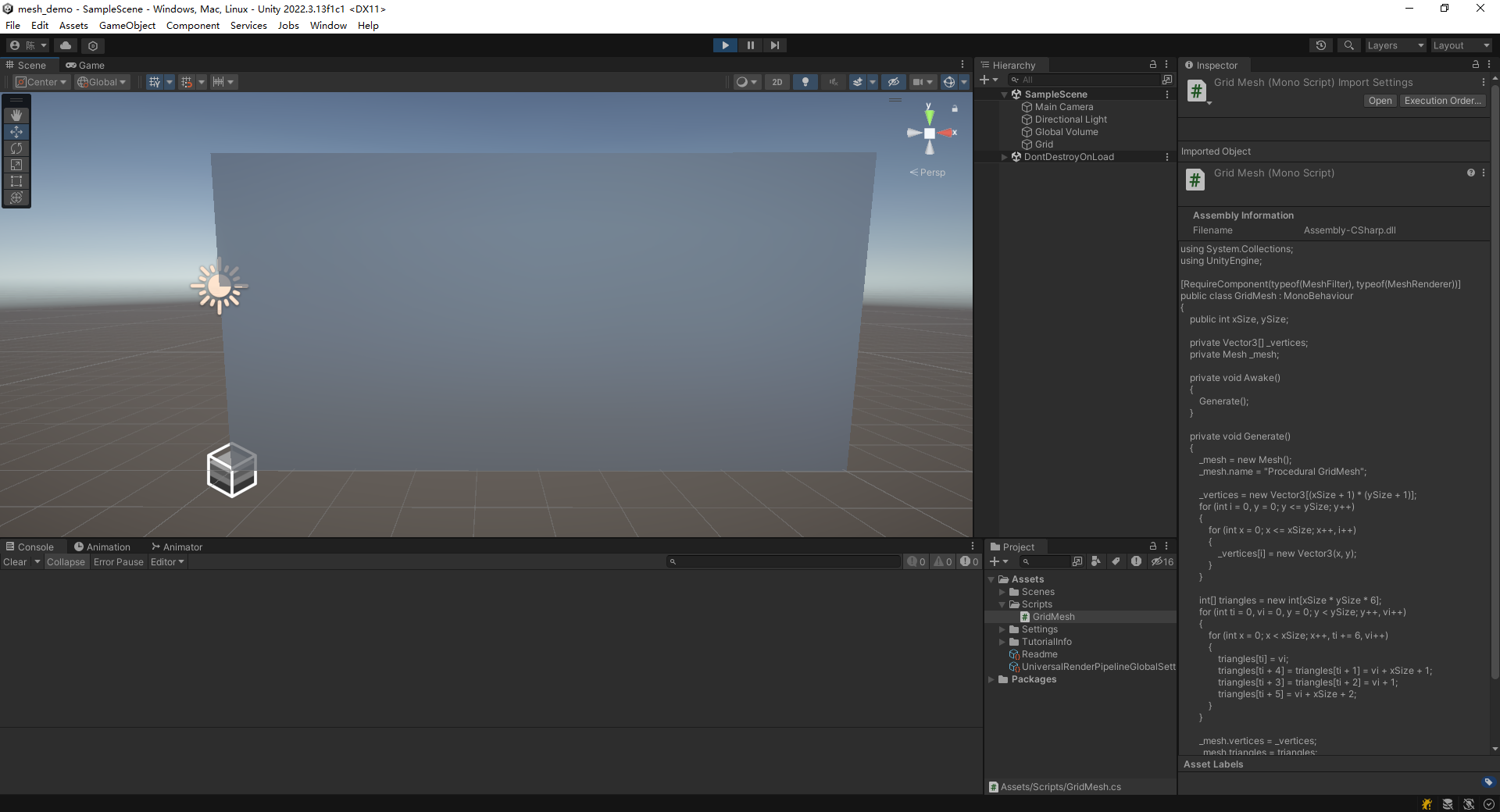
生成附加顶点数据
目前我们的 mesh 没有提供任何的法线信息,因此默认的法线方向都是 $(0,0,1)$ 。法线还可以用来确定光线击中表面的角度。
此处是由于我们的三角形都在同一个平面上,因此不需要单独提供额外的法线信息。而提供额外的法线信息是可以在不增加面数的前提下做出一些欺骗眼球的效果的,其实就是 GAMES101 作业当中法线贴图处的知识,不过这种法线贴图做出来的效果会在物体边缘露馅。
我们可以让网格根据其三角形来确定法线本身:1
_mesh.RecalculateNormals();
Mesh.RecalculateNormals 计算每个顶点的法线是通过计算哪些三角形与该顶点相连,先确定这些平面三角形的法线,对它们进行平均,最后对结果进行归一化处理。
我们先使用一下官网提供的 material,下载链接 ,如果使用了 urp 的话 convert 一下即可。
运行之后发现,我们的 uv 贴图并没有正确应用,都是纯色。

这是因为我们并没有提供 uv 坐标,其默认的都是 0,要使纹理适合我们的整个网格,只需将顶点的位置除以网格尺寸即可:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 _vertices = new Vector3[(xSize + 1) * (ySize + 1)];
Vector2[] uv = new Vector2[_vertices.Length];
for (int i = 0, y = 0; y <= ySize; y++)
{
for (int x = 0; x <= xSize; x++, i++)
{
_vertices[i] = new Vector3(x, y);
// 确保此处除法结果为浮点数
uv[i] = new Vector2((float)x / xSize, (float)y / ySize);
}
}
// 此处设置 uv,必须位于设置 vertices 之后,因为设置 uv 时会直接检查长度是否和 vertices 相同
_mesh.vertices = _vertices;
_mesh.uv = uv;
_mesh.triangles = triangles;
_mesh.RecalculateNormals();
GetComponent<MeshFilter>().mesh = _mesh;
可以看到纹理正常显示了:
其实还是有点不正常,因为我们网格大小设置的为 $10x5$ ,其会在水平方向上被拉伸,因此我们要改动一下 material 的 Tiling 的参数,改为 $(2,1)$ 。这样使得 u 坐标翻倍,我们纹理贴图的 Wrap Mode 被设置为 repeat 。就能看到两个方形瓦片。

法线贴图
另一种向表面添加更明显细节的方法是使用法线贴图,这个纹理上包含以颜色编码的法线向量。将它们应用到表面会产生比单用顶点法线更详细的光效应。所有的素材下载地址
但只将这种材质球应用到我们的网格中会产生凸起,是不正确的。我们需要在网格中添加切线向量来正确地定位它们。
切线是如何作用的:
- 法线映射是在切线空间中定义的。这是一个在物体表面流动的三维空间。这种方法允许我们在不同的地方和方向应用相同的法线映射。
切线向量和法线向量共同定义了切线空间。在理想情况下,切线向量和法线向量之间的夹角是90度,这样就形成了一个右手坐标系,其中法线向上,切线水平。这种情况下,切线向量和法线向量的叉乘就会得到一个垂直于表面的向量,即切线空间中的另一个轴,通常称为副法线(bitangent)。
在现实中,角度往往不是 90°,但结果仍然够好。所以切线是一个三维向量,但是 Unity 实际上使用了一个 4D 向量。它的第四个分量总是 −1 或 1 ,用于控制第三切线空间维的方向——前向或后向。这方便对法线映射进行镜像,这种映射经常用于像人这样具有双边对称性三维模型中。
Unity的着色器执行此计算的方式要求我们使用 −1。因为我们是一个平面,所以所有的切线都指向相同的方向,也就是右边。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32_vertices = new Vector3[(xSize + 1) * (ySize + 1)];
Vector2[] uv = new Vector2[_vertices.Length];
Vector4[] tangents = new Vector4[_vertices.Length];
Vector4 tangent = new Vector4(1f, 0f, 0f, -1f);
for (int i = 0, y = 0; y <= ySize; y++)
{
for (int x = 0; x <= xSize; x++, i++)
{
_vertices[i] = new Vector3(x, y);
uv[i] = new Vector2((float)x / xSize, (float)y / ySize);
tangents[i] = tangent;
}
}
int[] triangles = new int[xSize * ySize * 6];
for (int ti = 0, vi = 0, y = 0; y < ySize; y++, vi++)
{
for (int x = 0; x < xSize; x++, ti += 6, vi++)
{
triangles[ti] = vi;
triangles[ti + 4] = triangles[ti + 1] = vi + xSize + 1;
triangles[ti + 3] = triangles[ti + 2] = vi + 1;
triangles[ti + 5] = vi + xSize + 2;
}
}
_mesh.vertices = _vertices;
_mesh.uv = uv;
_mesh.tangents = tangents;
_mesh.triangles = triangles;
_mesh.RecalculateNormals();
GetComponent<MeshFilter>().mesh = _mesh;

参考:









